jmathanim
A Java library to make mathematical animations
Project maintained by davidgutierrezrubio Hosted on GitHub Pages — Theme by mattgraham
Constructible objects
Since version 0.9.5, JMathAnim has introduced constructible objects. These objects inherit from the abstract class Constructible which is itself a subclass of MathObject, so they have all the common properties of those, such as styling, for example.
A constructible object is a MathObject,that is built in a similar way as constructive geometry works. That’s it, computing parallels, intersections, etc. The main difference with a normal MathObject is that they depend on other Constructible objects, and most of them are “rigid” in the sense that they cannot be shifted, rotated, or scaled (well, they can, but with no effect). All Constructible objects have names with the prefix CT.
For example, the following code:
CTPoint A = CTPoint.make(Point.at(0, 0)).dotStyle(Point.DotSyle.CROSS).drawColor("blue");
CTPoint B = CTPoint.make(Point.at(1, 1)).dotStyle(Point.DotSyle.CROSS).drawColor("blue");;
CTSegment segment = CTSegment.make(A, B).drawColor("red").thickness(10);
CTPerpBisector perpBisector = CTPerpBisector.make(segment).drawColor("darkgreen").thickness(10);
CTCircle circle=CTCircle.makeCenterPoint(A, B).dashStyle(DashStyle.DASHED).drawColor("gray");
add(A, B, segment, perpBisector,circle);
play.shift(5, 0, -1, B);
waitSeconds(3);
Will give an animation like this:
In this example, we have created 2 CTPoint objects. These are almost identical to the classic Pointobject. The CTSegment object represents a segment between 2 CTPoint objects. Note that this object is not a Shape in the sense that you can transform it into another Shape for example, but it always remains as a segment. These objects are more rigid, but they allow for richer properties depending on the context.
The CTPerpBisector does as its name suggests, constructs the perpendicular bisector of the given segment.
Another object shown is the CTCircle. The static method makeCenterPoint(A,B) creates the circle with center A passing through point B.
Finally, we perform a shift animation to B. Note that all objects that depend on B are updated accordingly.
Each Constructible object has its own static constructor method with several parameters. For example, the CTPerpBisector allows a static constructor from a CTSegment but also with 2 CTPoint objects. Also, several builder methods that accept CTPoint are overloaded to accept Pointobjects (they simply wrap them into new CTPoint instances).
Constructible lines
The class CTLine has several subclasses such as CTRay, CTSegment, CTAngleBisector, CTLineOrthogonal, CTPerpBisector, or CTVector. These are fairly self-explanatory, but one thing they have in common is that they all implement the interface hasDirection means that this object has an inherent direction (not oriented). So, we can use any of these objects as a parameter that admits a direction. For example, we can build a orthogonal line that passes through a CTPoint and is perpendicular to a CTLine, CTSegment, or CTVector. Other non-constructible objects, like Line, Ray or Arrow2D also implement this interface.
CTLaTeX
Mostly like his brother-in-code, LaTeXMathObject, this object represents a LaTeX string to be drawn on screen. This object is permanently stacked at a given CTPoint. We’ll see an example of this class in the next section.
CTIntersection
The CTIntersection object extends the CTPoint object and represents the intersection point between two constructible objects. In the current version, several static builders can be used:
CTIntersectionPoint p1=CTIntersectionPoint.make(ct1,ct2,num);
Where ct1 and ct2 can be CTLine, CTSegment, CTRay and CTCircle. In the case of intersecting with a circle, the intersection may be 2 points. The num variable (1 or 2) determines the solution number.
For example, the following code:
CTPoint A = CTPoint.at(.3, .0).drawColor("blue");
CTPoint B = CTPoint.at(-.5, -.1).drawColor("red");
CTLine toIntersect = CTLine.make(A, B);
CTCircle circle = CTCircle.makeCenterRadius(Point.origin(), 1);
CTIntersectionPoint inter1 = CTIntersectionPoint.make(circle, toIntersect, 1).drawColor("green");
CTIntersectionPoint inter2 = CTIntersectionPoint.make(circle, toIntersect, 2).drawColor("yellow");
add(A, B, toIntersect, circle, inter1, inter2);
add(//Let's add some labels
CTLaTeX.make("$A$", A, Anchor.Type.DL, .02).scale(.5),
CTLaTeX.make("$B$", B, Anchor.Type.DL, .02).scale(.5),
CTLaTeX.make("$1$", inter1, Anchor.Type.DL, .02).scale(.5),
CTLaTeX.make("$2$", inter2, Anchor.Type.DL, .02).scale(.5)
);
waitSeconds(3);
It generates the following image with the 2 solutions numbered. Which solution number should we choose? If we parametrize the line AB where A is at t=0 and B is at t=1, and the intersections are located at parameter t1 and t2, then solution number 1 is at min(t1,t2) and number 2 is at max(t1,t2):
If there is no intersection, the point returned will have coordinates Double.NaN. You can check if any of the coordinates a point is NaN with the Vec method isNaN().
CTPoint P=....
if (P.v.isNan()) {
//Sorry mate, at least one coordinate is NaN...
}
Converting to non-constructible MathObjects
Suppose you have built a CTCircle that passes through 3 points, but now you want to transform it into a square. You cannot do that with a Constructible object (in fact, it will give you an error), but you can extract the contained MathObject which is actually drawn and perform any transformation to it.
//With the layer(1) we ensure the dots are over the rest of the objects
CTPoint A= CTPoint.at(0, 0).drawColor("blue").thickness(60).layer(1);
CTPoint B= CTPoint.at(1, 0).drawColor("red").thickness(60).layer(1);
CTPoint C= CTPoint.at(.75, .75).drawColor("green").thickness(60).layer(1);
CTCircle circle = CTCircle.make3Points(A,B,C).style("solidred");
add(A,B,C,circle);
//Let's move the C point for fun!
play.shift(2,0,-.5,C);
//The next command is necessary! Doing so it will remove an unused object from the scene
//but more importantly, it will unregister the CTCircle from the update queue
//and stop updating the contained MathObject, leaving it "free".
remove(circle);
Shape shape=circle.getMathObject();
play.transform(3, shape, Shape.square().style("solidblue"));
waitSeconds(3);
Geogebra import
One of the advantages of Constructible objects is that they behave similarly to the objects of the Geogebra program. In the rare case you don’t know it, Geogebra is an excellent open source software that allows you to do geometric constructions (and many other things). JMathAnim can import Geogebra files in a limited way (keep in mind that Geogebra has literally hundreds of commands!). For now, the following elements can be successfully imported: points, midpoints, intersections (of lines, rays, segments, circles), lines, orthogonal, parallel, perpendicular bisectors, polygons, regular polygons, vectors, mirrored, translated, and rotated points. JMathAnim will log a warning when it finds an unknown command that cannot be imported. The process is quite simple. For example, suppose we have a document like this created in Geogebra, where we have calculated the circumcenter of a triangle, drawing the 3 perpendicular bisectors:
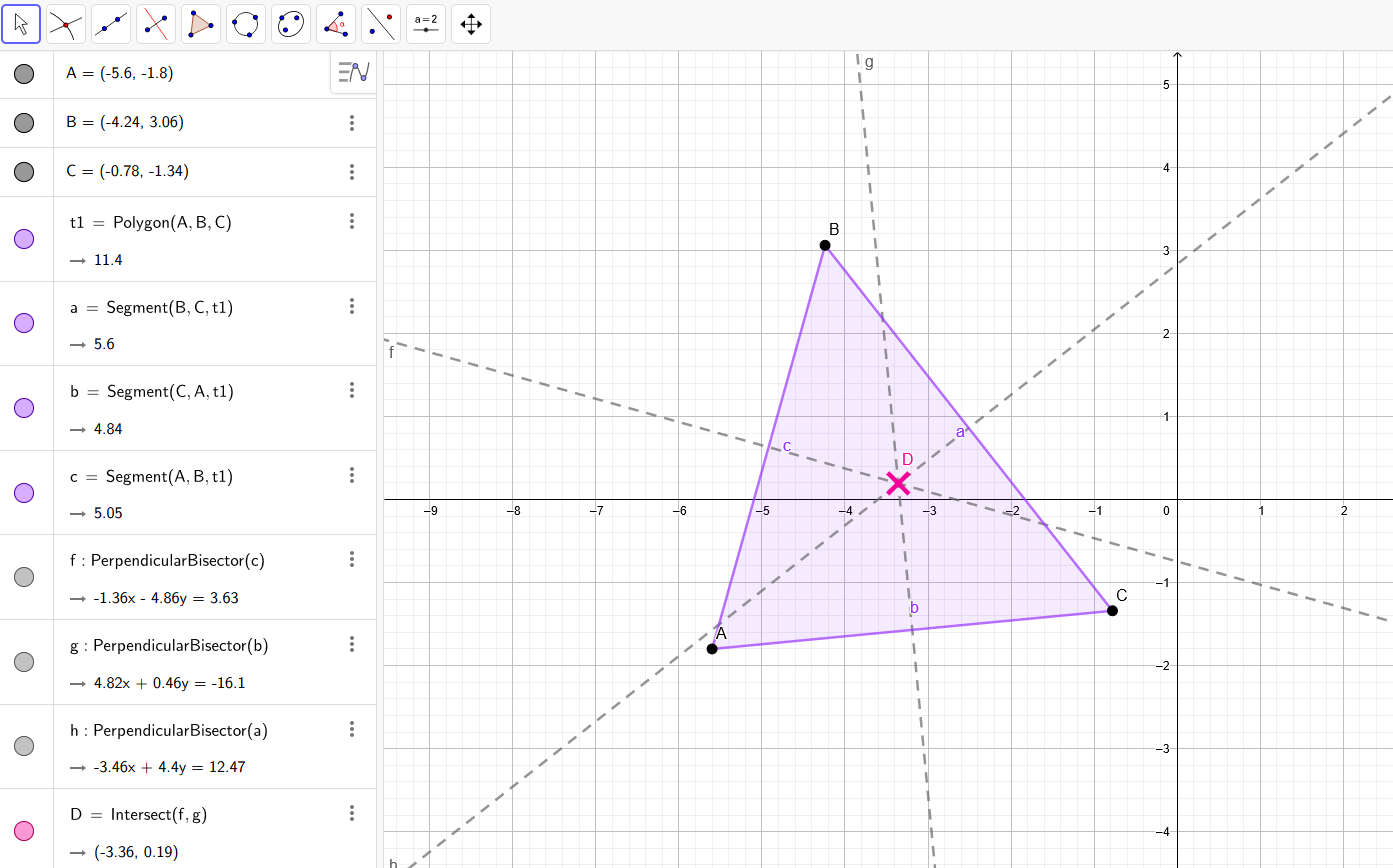
Now, we save this in our disk under the name test.gbb, in a directory named resources/geogebra of our project. This will be the default location for Geogebra files (remember, you can change this behavior with the # and ! flags).
//With this command we parse the file resources/geogebra/test.gbb
GeogebraLoader gl = GeogebraLoader.parse("test.ggb");
Now, JMathAnim will try to convert all Geogebra elements, logging a warning if there is an unknown command (and possibly throwing an exception if there are objects that depend on this unknown object). If all goes well, the gl object will have a Dictionary with the created objects.
The command
add(gl);
This is equivalent to adding all the imported objects to the scene.
If you want to adjust the camera to the view of the original Geogebra document, you can do this with the command:
camera.setViewFrom(gl);
Note that the proportions may not be the same, so the view is approximate.
The imported document will look like this:
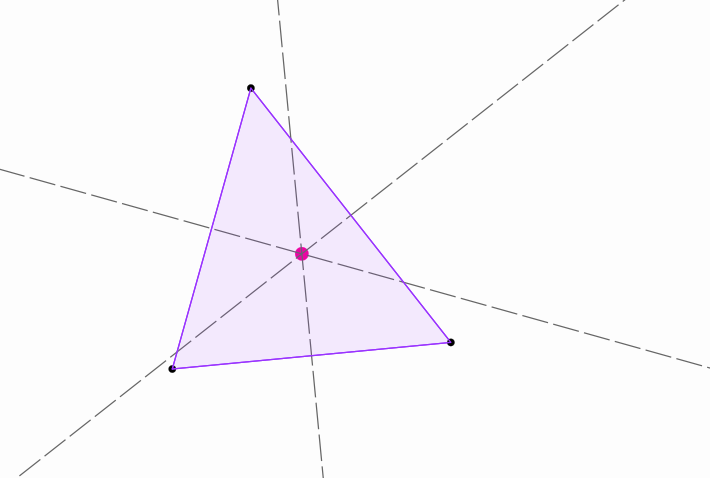
Not bad, right? Note that axis and object labels are not imported. And that’s it! Well, not really. If you want to animate elements or simply access them, you can use the original names that these objects had in Geogebra. For example, to access point A, you can use the command
gl.get("A");
Now, let’s add some animations to the creation of this scene to make it cooler!
GeogebraLoader gl = GeogebraLoader.parse("test.ggb");
camera.setViewFrom(gl);
playAnimation(
Commands.moveIn(1,Anchor.Type.LEFT, gl.get("A")),
Commands.moveIn(1,Anchor.Type.UPPER, gl.get("B")),
Commands.moveIn(1,Anchor.Type.RIGHT, gl.get("C"))
);
play.showCreation(gl.get("t1"));
play.showCreation(gl.get("f"),gl.get("g"),gl.get("h"));
play.moveIn(Anchor.Type.UPPER, gl.get("D"));
waitSeconds(3);
Limitations
Currently JMathAnim can import most common geometric constructions, but there are other elements that cannot be imported yet. For example, any element that is built from an algebraic expression given in a string cannot be imported. This applies to functions or points whose coordinates are not numbers but formulas.