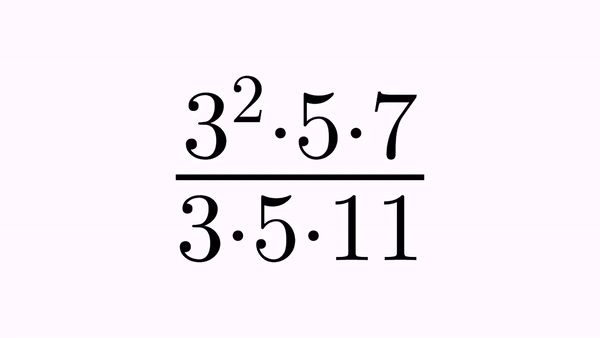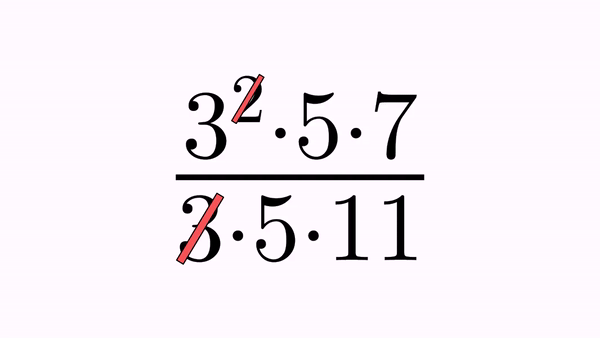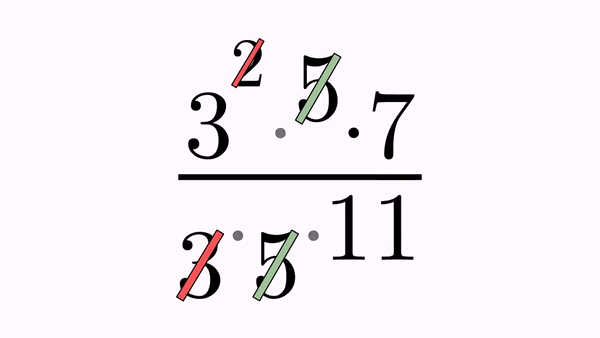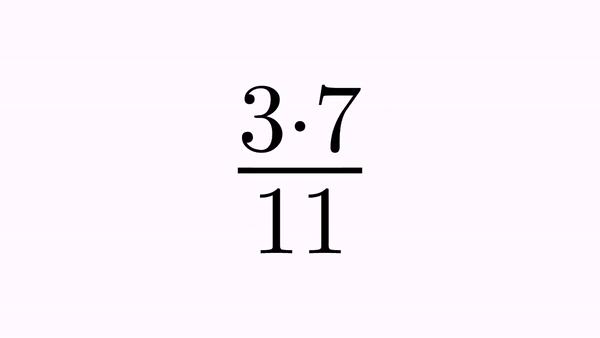jmathanim

A Java library to make mathematical animations

---

Project maintained by davidgutierrezrubio Hosted on GitHub Pages — Theme by mattgraham

Mathematical formulas

As we have seen, math formulas are created with the LaTexMathObject class. Since version 0.9.5-SNAPSHOT, the LaTeX code is compiled using the library JLaTeXMath removing the need to have a working LaTeX distribution installed in the system. All glyphs generated are converted into Shapeobjects.

For example, if we generate a math expression with the command

LatexMathObject sum=LatexMathObject.make("$2+2=4$");

It will generate 5 shapes, that we can access via the get method. Thus, the command sum.get(0) will return the first shape (the “2” glyph), sum.get(1) will return the “+” glyph, etc. These indices will be important to specify exactly how we want the animation from one expression to another to be done.

The major drawback of this approach is that it is not always clear which glyph of the formula corresponds to a given index. For that, we have the method formulaHelper that takes a varargs of LatexMathObject objects, or String with the LaTeX code, overlays the shape number for each one, stacks the formulas vertically, zooms and adds them to the scene. For example:

LatexMathObject t1 = LatexMathObject.make("$e^{i\\pi}+1=0$");
LatexMathObject t2 = LatexMathObject.make("$\\sqrt{a+b}\\leq\\sqrt{a}+\\sqrt{b}$");
formulaHelper(t1, t2);
waitSeconds(5);

We’ll obtain the following image for 5 seconds. You can make a screenshot or save it to a file with the saveImage command to examine it more deeply:

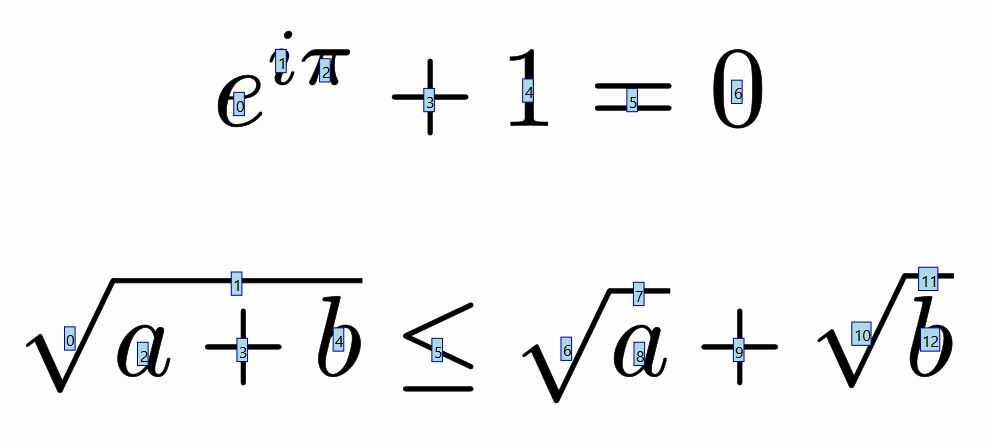
It is recommended, before doing any animation that involves math formulas, to run this method to get useful references when defining animations.

Setting color to specific parts of a math expression

If you want to apply colors to some parts of a math expression, you can use the \color commands of LaTeX or you can use the setColorToIndicesmethod and specify the indexes to apply the color. For example:

LatexMathObject formula=LatexMathObject.make("$(a+b)^2=a^2+b^2+2ab$").center();
camera.adjustToAllObjects();
formula.setColorsToIndices(JMColor.parse("darkred"),1,7,14);//Color dark red to indexes 1, 7 and 14
formula.setColorsToIndices(JMColor.parse("darkgreen"),3,10,15);//Color dark green to indexes 3,10 and 15
add(formula);
waitSeconds(5);

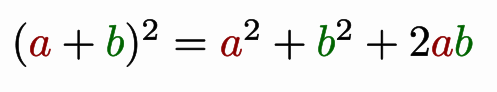
Note that the method changes both draw and fill colors. Since version 0.9.11 there is another, easier way to automatically assign colors, which we will see in the next chapter.

The slice method

Sometimes you may need to separate a formula into parts so you can animate them separately. The slice method extracts a subformula with the given indexes and removes the extracted shapes from the original formula. For example, suppose we have the formula $A=b\cdot h$ and want to initially show the “b” and “h” glyphs in a rectangle before putting them in their original place:

  Shape rectangle = Shape.square().scale(2,1).center().fillColor("chocolate");
        LatexMathObject formula = LatexMathObject.make("$A=b\\cdot h$")
                .layer(1)
                .stack()
                .withGaps(.1)
                .toScreen(ScreenAnchor.UPPER);

        formula.setColorsToIndices("steelblue",2);
        formula.setColorsToIndices("crimson",4);

        LatexMathObject sliceBase=formula.slice(2);//Extracts the "b" from the formula
        LatexMathObject sliceHeight=formula.slice(4);//Extracts the "h from the formula

        Vec sliceBaseCenter=sliceBase.getCenter();//Save the centers into these variables
        Vec sliceHeightCenter=sliceHeight.getCenter();

//Position the sliced parts in the rectangle
        sliceBase
                .stack()
                .withDestinyAnchor(AnchorType.LOWER)
                .withGaps(.1)
                .toObject(rectangle);
        
        sliceHeight
                .stack()
                .withDestinyAnchor(AnchorType.RIGHT)
                .withGaps(.1)
                .toObject(rectangle);

        play.showCreation(rectangle, sliceBase,sliceHeight);
        play.showCreation(formula);//Draws the formula, except "b" and "h"
        scene.waitSeconds(1);
        ShiftAnimation anim1 = Commands.moveTo(3, sliceBaseCenter, sliceBase);
        ShiftAnimation anim2 = Commands.moveTo(3, sliceHeightCenter, sliceHeight);
        playAnimation(anim1,anim2);//Restores the slices to their original positions
        waitSeconds(2);

Note that, although the sliced formula has only one element, the indexes remain the same. So, if the “b” glyph was in position 2 in the original formula, it is still in position 2 in the sliced formula. Consequently, the method sliceBase.get(2) returns the “b” shape. The other indexes store empty shapes.

There is another version of the method, with a boolean flag that controls if the sliced shapes are removed from the original math expression or not. In the preceding example, LatexMathObject sliceBase=formula.slice(false,2) will generate a slice of the “b” glyph without changing the original formula.

The slicemethod can be a powerful tool if you want to operate on parts of complex math expressions. If you want to progressively show a complex formula, the easiest option is to slice it into the different parts you will be showing at a concrete point in the animation. For example, suppose we want to progressively show the first terms of the Taylor expansion of sin(x). We have the following LaTeX code:

 String taylorLatexCode="$$\\sin x = x - " +
               "\\frac{x^3}{3!} + " +
               "\\frac{x^5}{5!} - " +
               "\\frac{x^7}{7!} +" +
               " \\frac{x^9}{9!} " +
               "-\\frac{x^{11}}{11!} \\cos(\\xi), \\qquad \\xi \\in (0, x)$$";

The method formulaHelper(taylorLatexCode)shows in screen the indexes of the formula. You can save it to a file with the saveImagemethod or just have the program to wait with waitSecondstime enough to make a screenshot and have the following:

As you can see, the formula has 52 elements. We are interested in the start and end indexes of the terms, and using the slicemethod we will separate the formula in parts:

String taylorLatexCode="$$\\sin x = x - " +
    "\\frac{x^3}{3!} + " +
    "\\frac{x^5}{5!} - " +
    "\\frac{x^7}{7!} +" +
    " \\frac{x^9}{9!}" +
    "-\\frac{x^{11}}{11!} \\cos(\\xi), \\qquad \\xi \\in (0, x)$$";
LatexMathObject taylor = LatexMathObject.make(taylorLatexCode);
camera.adjustToObjects(taylor);//Ensure that the camera captures all

ArrayList<LatexMathObject> formulaParts = new ArrayList<>();

//Note that IntStream.range(0,5).toArray() is equivalent to 0, 1, 2, 3, 4
formulaParts.add(taylor.slice(IntStream.range(0,5).toArray()));//The "sin(x)=" part
formulaParts.add(taylor.slice(5));//The first term ("x")
formulaParts.add(taylor.slice(IntStream.range(6,12).toArray()));//The second term ("+x^2/2!")
formulaParts.add(taylor.slice(IntStream.range(12,18).toArray()));//The third term
formulaParts.add(taylor.slice(IntStream.range(18,24).toArray()));//The fourth term
formulaParts.add(taylor.slice(IntStream.range(24,30).toArray()));//The fifth term
formulaParts.add(taylor.slice(IntStream.range(30,45).toArray()));//The remainder term, part 1
formulaParts.add(taylor.slice(IntStream.range(45,52).toArray()));//The remainder term, part 2

//Now we can work on each term individually
for (LatexMathObject t:formulaParts) {
    play.showCreation(t);
    scene.waitSeconds(1);
}
scene.waitSeconds(3);

Animating transforms between equations

Suppose we are planning to perform an animation that solves a simple equation x+2=0. We define the two math expressions:

LatexMathObject t1=LatexMathObject.make("$x+2=0$");
LatexMathObject t2=LatexMathObject.make("$x=-2$");

and we want to define a precise, self-explanatory animation, that transforms the first equation into the second.

If we simply try the command

play.transform(4, t1, t2);

we will obtain the following animation:

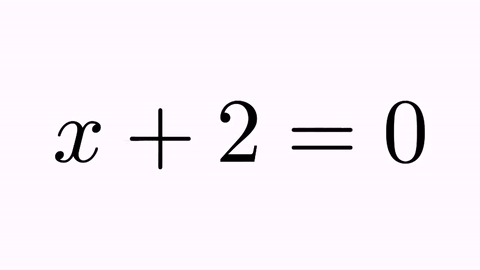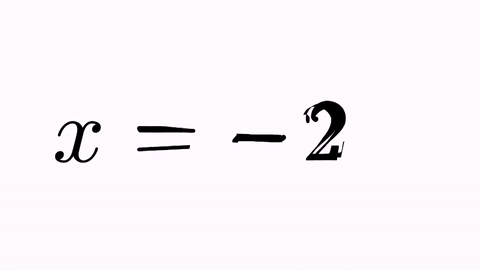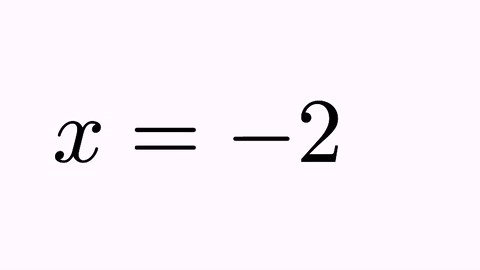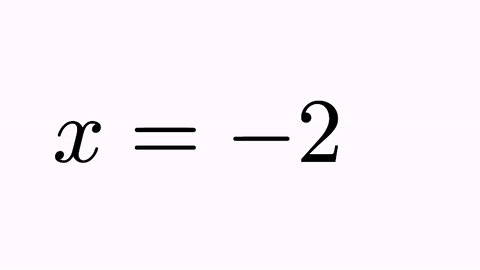
It’s nice, but not illustrative. It would be better to force the “+2” to convert into “-2”, and the original “x” and “=” glyphs to their counterparts “x” and “=” glyphs. For this, we have the TransformMathExpression animation class. But first, we must be clear about the indexes of the different shapes that compose the latex objects. For that, we use the method formulaHelper:

formulaHelper(t1,t2);
waitSeconds(5);

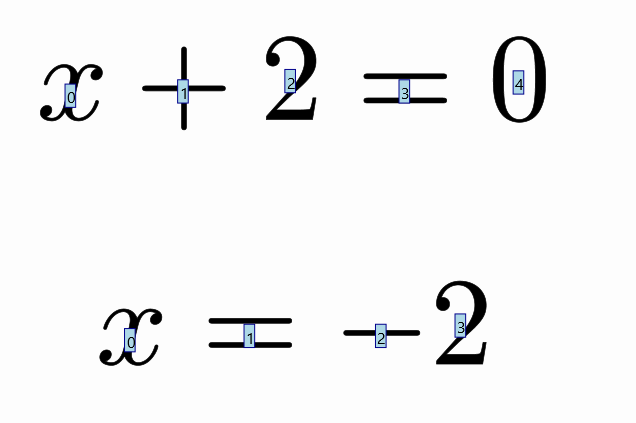
So, we need an animation that maps shape 0 onto shape 0, shape 3 onto shape 1, etc.

We create a new TransformMathExpression animation object, with the expected parameters:

TransformMathExpression tr = TransformMathExpression.make(5, t1, t2);

The TransformMathExpression objects admits several commands to define the precise transform we want to do. In this case, we want to transform the original shape 0 (x) to destiny shape 0 (x). This is stated with the commandmap

tr.map(0,0);//Transforms orig-shape 0 to dst-shape 0

We also want to map the “+” sign (shape 1) into the “-“ sign (shape 2), with the command

tr.map(1,2);//Transforms orig-shape 1 to dst-shape 2

and the original “2” (shape 2) into the destiny “2” (shape 3):

tr.map(2,3);

And finally, the “=” sign (shape 3) into the another “=” sign (shape 1):

tr.map(3,1);//Transforms orig-shape 3 to dst-shape 1

What about shape 4 (the “0” sign)? If we don’t specify a destination, this shape is marked for removal, with a fadeOut animation by default. If we play this animation with the playAnimation method we have:

LatexMathObject t1=LatexMathObject.make("$x+2=0$");
LatexMathObject t2=LatexMathObject.make("$x=-2$");
TransformMathExpression tr=TransformMathExpression.make(5, t1, t2);
tr.map(0,0);//Transforms orig-shape 0 to dst-shape 0
tr.map(1,2);//Transforms orig-shape 1 to dst-shape 2
tr.map(2,3);
tr.map(3,1);//Transforms orig-shape 3 to dst-shape 1
playAnimation(tr);

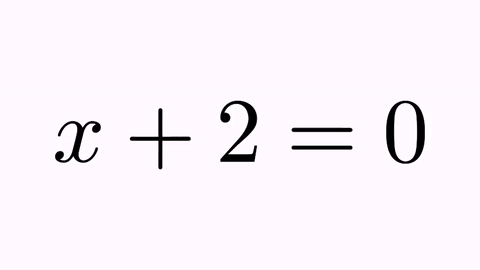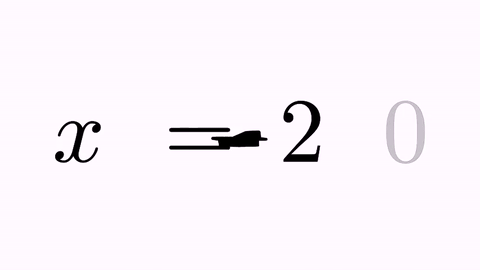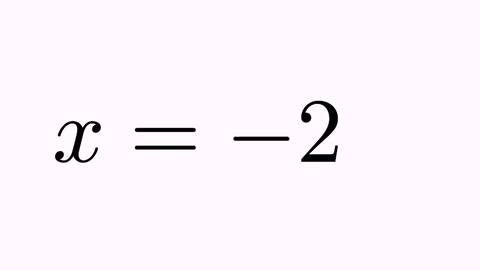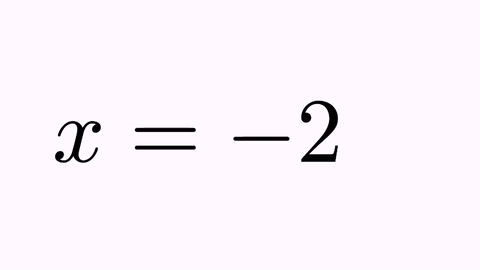
Ok, this is better, but there is still something that looks odd. When manipulating equations, it’s always desirable to mark the “=” sign as a pivotal point. We can achieve this by forcing that the origin and destiny formulas are aligned by the “=” sign. This sign is at position 3 in the origin formula and at position 1 in destiny. With the command

    t2.alignCenter(1, t1, 3);

we make that the center of glyph number 1 of t2 (its “=” sign) matches the center of the glyph number 3 of t1 (its “=” sign). If we execute this method prior to the animation now we have:

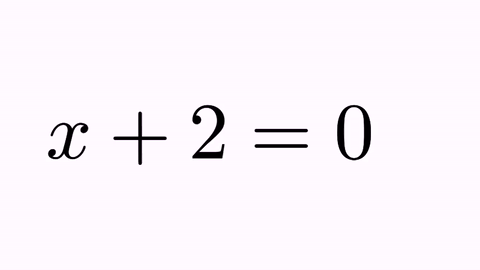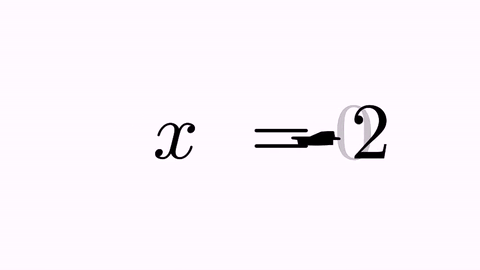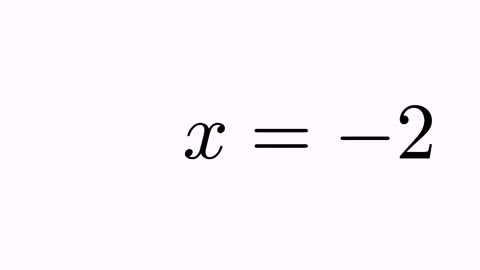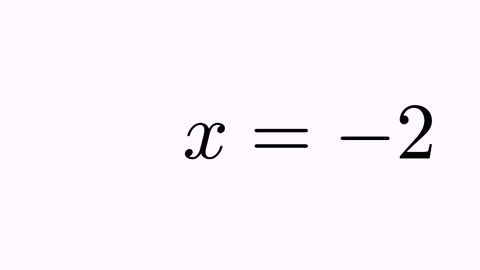
Disclaimer: This is not, by far, the best way to show the resolution of an equation like this! I show this specific animation for a better understanding of the program.

Type of transformations

The .map method returns a TransformMathExpressionParameters object, which allows us to control how the transformation is done, with the method setTransformStyle. Transformation types are defined in the enum TransformMathExpression.TransformType, currently INTERPOLATION, FLIP_HORIZONTALLY, FLIP_VERTICALLY and FLIP_BOTH. By default, the INTERPOLATION method is used.

Note: The INTERPOLATION method uses the Transform class to do the work, so, depending on the origin and destination shapes, it may actually perform a point-to-point interpolation, or, if applicable, an isomorphism or a more general affine transform. For example, if you use an INTERPOLATION type transform to map a “2” character to another “2”, it will use an isomorphism, since these 2 characters are the same except for scale.

LatexMathObject t1 = LatexMathObject.make("$a^2=a\\cdot a$");
LatexMathObject t2 = LatexMathObject.make("$3^2=3\\cdot 3$");
t1.alignCenter(2, t2, 2);//Move t1 so its equal sign (glyph 2) matches the t2 equal sign (glyph 2)
camera.zoomToObjects(t1, t2);
TransformMathExpression tr = TransformMathExpression.make(5, t1, t2);
tr.map(0, 0).setTransformStyle(TransformMathExpression.TransformType.FLIP_HORIZONTALLY);//The first "a"
tr.map(1, 1);
tr.map(2, 2);
tr.map(3, 3).setTransformStyle(TransformMathExpression.TransformType.FLIP_VERTICALLY);//The second "a"
tr.map(4, 4);
tr.map(5, 5).setTransformStyle(TransformMathExpression.TransformType.FLIP_BOTH);//The third "a"
playAnimation(tr);
waitSeconds(3);

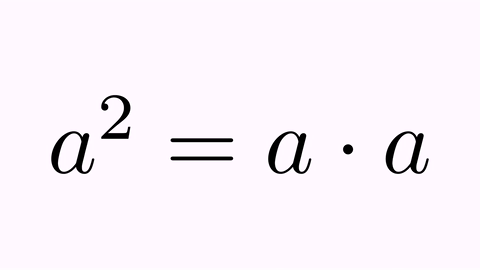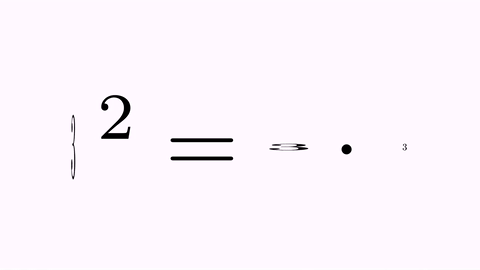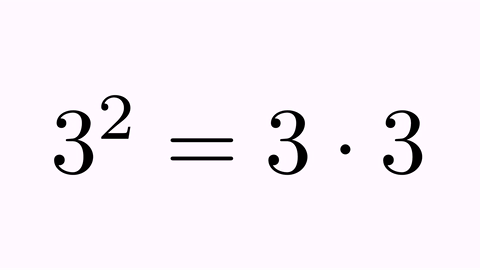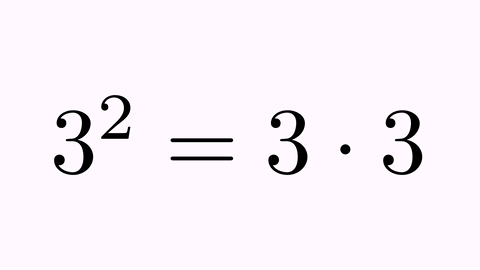
Range mapping

If we need to map a bunch of consecutive origin indexes into another bunch of consecutive destiny indexes , the method mapRange(OrigA,OrigB,dst) does exactly this. The command

tr.mapRange(3,7,13);

is equivalent to

tr.map(3,13);
tr.map(4,14);
tr.map(5,15);
tr.map(6,16);
tr.map(7,17);

Or, if you have two formulas with the same number of glyphs and one-to-one correspondence, the mapAll() method does all the work for you.

Grouping

Suppose we have the following two arithmetic expressions

LatexMathObject t1 = LatexMathObject.make("$(1+98)+(2+97)+\\cdots+(49+50)$");
LatexMathObject t2 = LatexMathObject.make("$99+99+\\cdots+99$");

and we want to animate how these sums change all into 99. We want to perform a transform for each one of the sums into their simplified form. Our dear friend formulaHelper helps us to elaborate a plan:

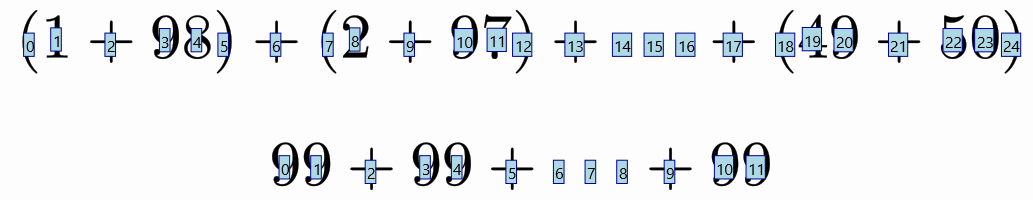
We are interested in mapping 0-5 origin indices to 0,1 destiny indices, 7-12 to 3,4 and 18-24 to 10,11. But in all these cases this means mapping 6 indices to 2. The map method only maps one index to another. To achieve this, we can define source and destination groups. We will use the 3 transform methods to show you the effect:

LatexMathObject t1 = LatexMathObject.make("$(1+98)+(2+97)+\\cdots+(49+50)$");
LatexMathObject t2 = LatexMathObject.make("$99+99+\\cdots+99$");
TransformMathExpression tr=TransformMathExpression.make(10, t1, t2);

//Define groups of first sum. You can use any string as name of the group, as long as it doesn't start with "_"
tr.defineOrigGroup("sum_1", 0,1,2,3,4,5);
tr.defineDstGroup("99_1", 0,1);
tr.map("sum_1","99_1").setTransformStyle(TransformMathExpression.TransformType.FLIP_HORIZONTALLY);

tr.map(6,2);//The first "+" sign

//Define groups of second sum
tr.defineOrigGroup("sum_2", 7,8,9,10,11,12);
tr.defineDstGroup("99_2", 3,4);
tr.map("sum_2","99_2").setTransformStyle(TransformMathExpression.TransformType.FLIP_VERTICALLY);

tr.mapRange(13, 17, 5);//The "+...+" part

//Define groups of third sum
tr.defineOrigGroup("sum_3", 18,19,20,21,22,23,24);
tr.defineDstGroup("99_3", 10,11);
tr.map("sum_3","99_3").setTransformStyle(TransformMathExpression.TransformType.INTERPOLATION);
playAnimation(tr);
waitSeconds(1);

Here is the gif of the generated video. As you can see, grouping allows a bunch of indices to be managed as a single object. When applying the INTERPOLATION transformation method, the MultiShapeTransform is used, which handles correctly when the number of origin and destination shapes does not match.

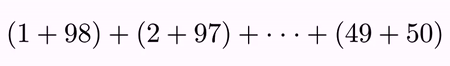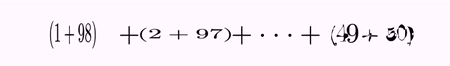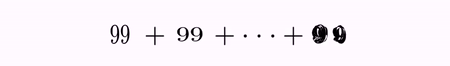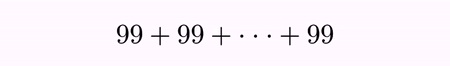
Effects

Each mapping from one shape (or group) to another can be decorated with some effects. These can be added right after the map command with the following methods. Let’s show them with an example. Suppose we want to animate the commutative property of the sum. Define the 2 LaTexMathObject objects and make an animation:

LatexMathObject t1=LatexMathObject.make("$a+b$");
LatexMathObject t2=LatexMathObject.make("$b+a$");
t2.alignCenter(1, t1, 1);//Align both expressions in the "=" sign
camera.zoomToObjects(t1,t2);
TransformMathExpression tr=TransformMathExpression.make(5, t1, t2);
tr.map(1,1);//= into =
tr.map(0,2);//a into b
tr.map(2,0);//b into a
playAnimation(tr);
waitSeconds(1);

We have the following animation:

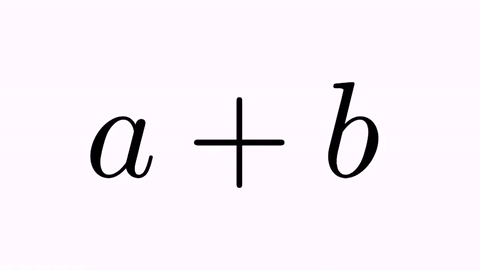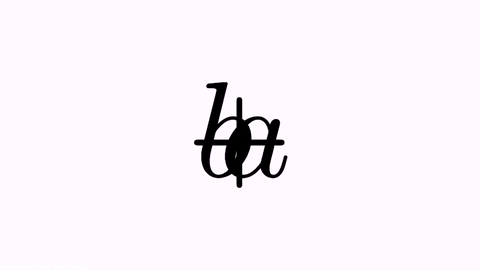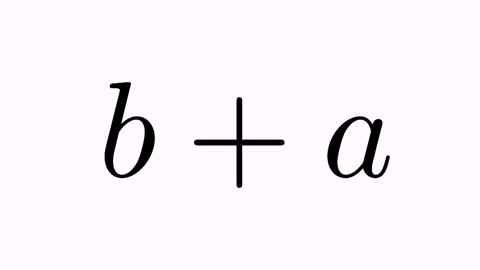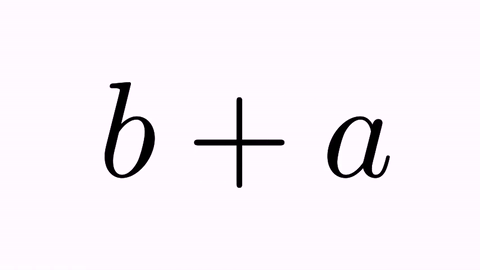
We will apply effects by adding them to the tr.map(0,2) and tr.map(2,0) commands. First, the .addScaleEffect(t) applies a scaling factor back and forth.

tr.map(0,2).addScaleEffect(.7);
tr.map(2,0).addScaleEffect(1./.7);

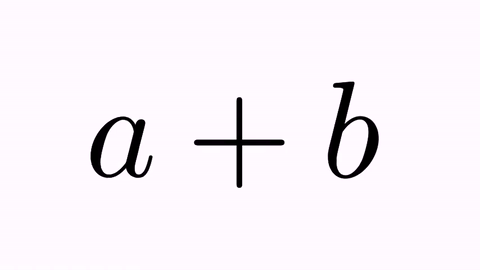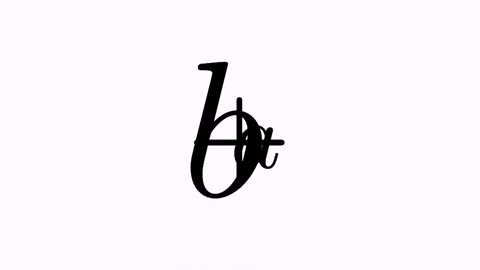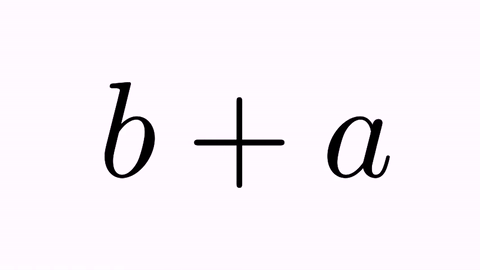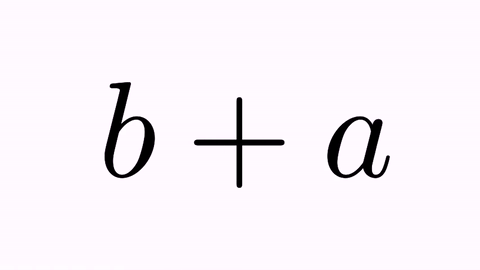
The .addAlphaEffect(t) changes the alpha (draw and fill) back and forth:

tr.map(0,2).addAlphaEffect(.7);
tr.map(2,0).addAlphaEffect(.7);

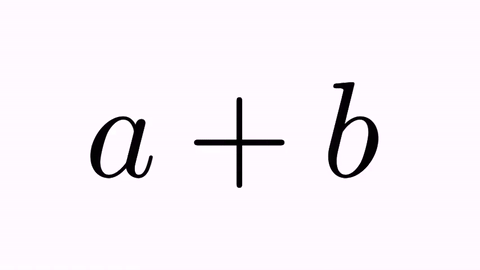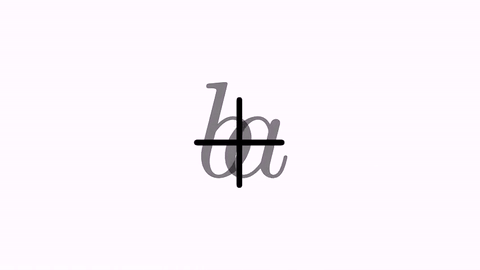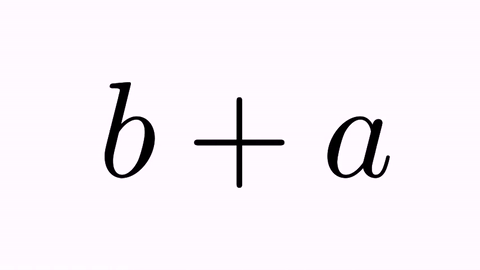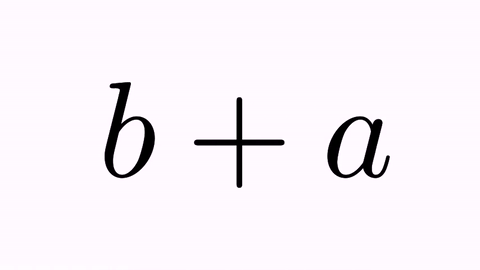
The .addRotateEffect(n) rotates n times the shape.

tr.map(0,2).addRotateEffect(1);
tr.map(2,0).addRotateEffect(-1);

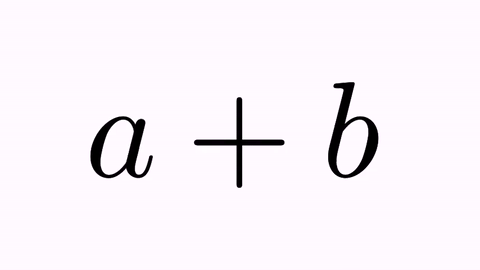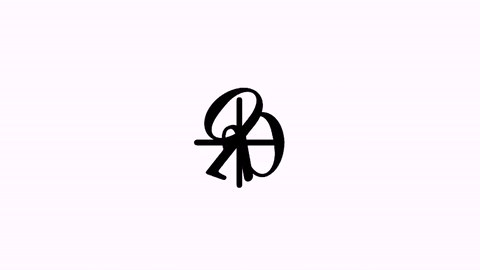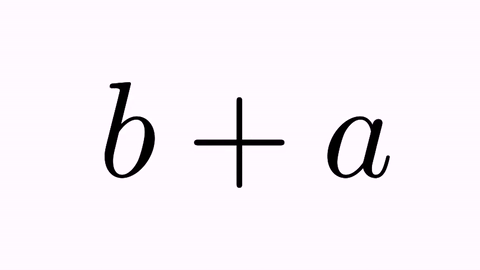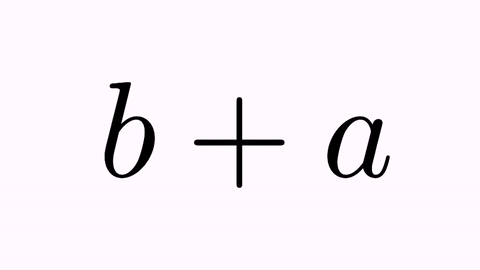
The .addJumpEffect(t) applies a jump with a vector of 90º clockwise.

tr.map(0,2).addJumpEffect(1);
tr.map(2,0).addJumpEffect(1);//Note that this "jump" is downward

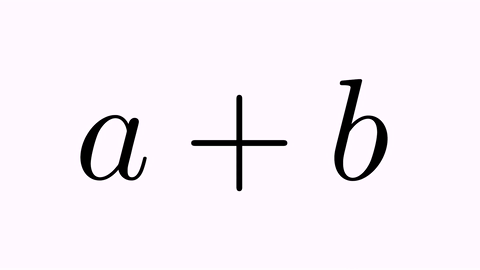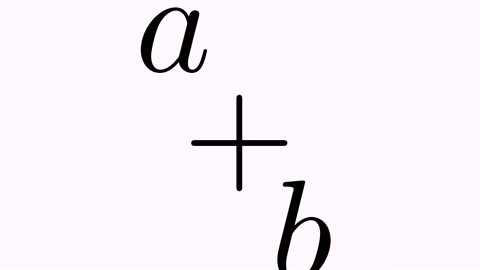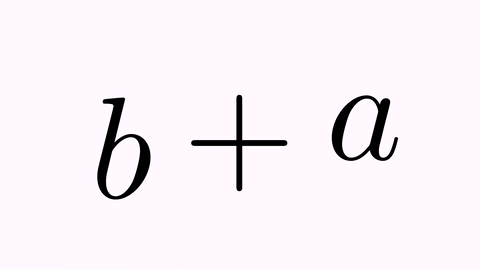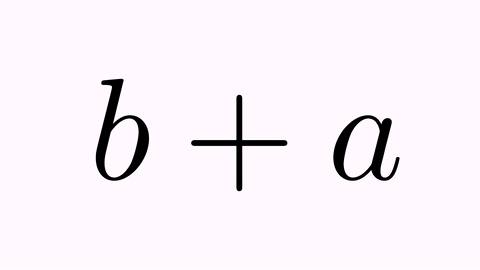
By default, the shape of the jump is a semicircle, so that only the sign of the parameter is relevant. Other jump types can be specified since version 0.9.0, defined in the enum AnimationEffect.JumpType: SEMICIRCLE, PARABOLICAL, ELLIPTICAL, TRIANGULAR, SINUSOIDAL, SINUSOIDAL2, CRANE. These are explained in detail in the animation effects chapter. For example, you can set it so that the “a” glyph moves like a crane grabs it, and that the “b” glyph follows a path resembling a triangular roof, with the following code:

tr.map(0, 2).addJumpEffect(t1.getHeight(), JumpType.CRANE);
tr.map(2, 0).addJumpEffect(t1.getHeight(), JumpType.TRIANGULAR);//Note that this "jump" is downward

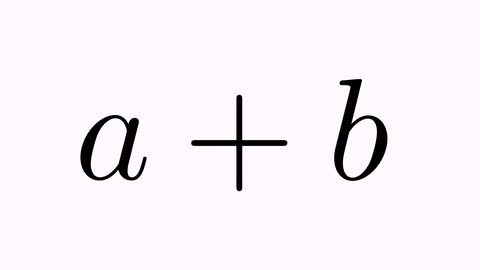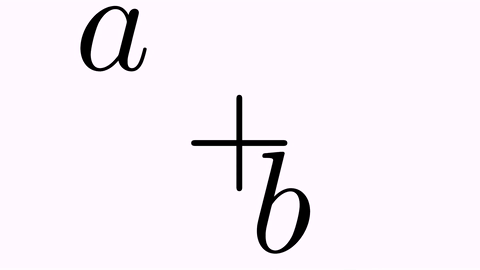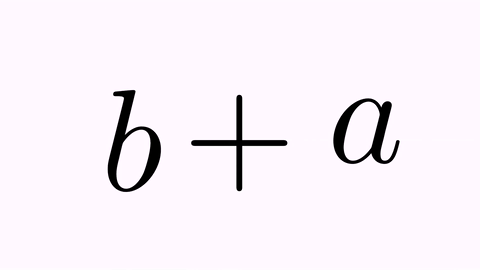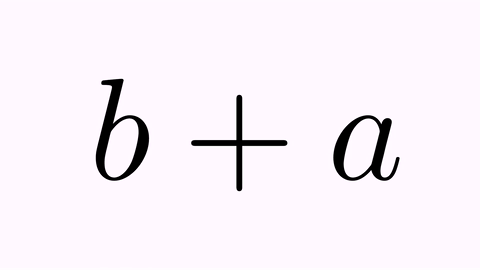
We use the method getHeight() to get the actual height of the formula, which will be the height of the jumps.

And, finally, you can nest any of these effects:

tr.map(0,2).addJumpEffect(.1).addRotateEffect(-1).addScaleEffect(.5);
tr.map(2,0).addJumpEffect(.1).addRotateEffect(1).addScaleEffect(.5);

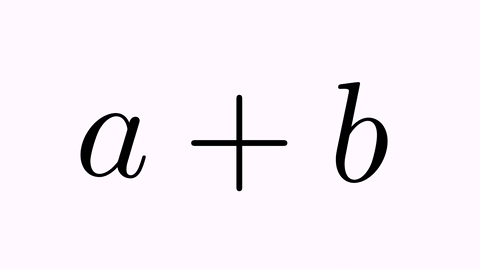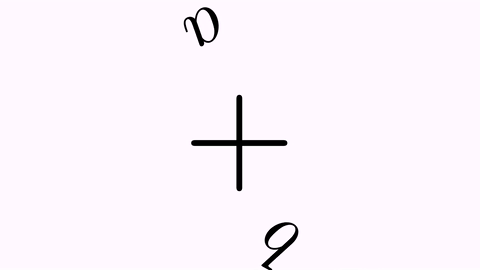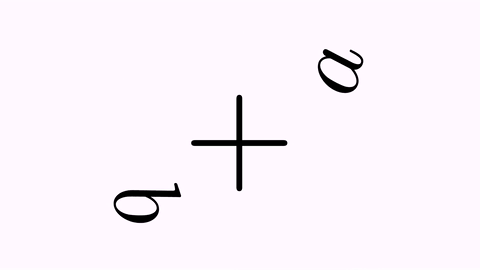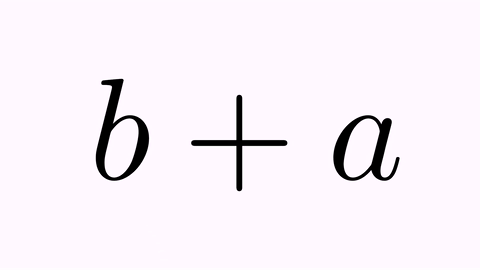
Shapes marked for removal or adding

Any shape whose index is not mapped to a destiny index or group is marked for removal. Currently, there are 6 types, defined in the enum TransformMathExpression.RemoveType: FADE_OUT, SHRINK_OUT, MOVE_OUT_UP, MOVE_OUT_LEFT, MOVE_OUT_RIGHT, MOVE_OUT_DOWN.

Similarly, any destiny shape that is not mapped by a origin index or group is marked for adding with one of the following ways, defined in the enum TransformMathExpression.AddType: FADE_IN, GROW_IN, MOVE_IN_UP, MOVE_IN_LEFT, MOVE_IN_RIGHT, MOVE_IN_DOWN.

By default, FADE_OUT and FADE_IN are chosen for removing and adding. With the setRemovingStyle and setAddingStyle we can define individually the style for each shape.

We’ll show all of this in one single, beautiful, self-explicative, dizzying animation:

LatexMathObject t1 = LatexMathObject.make("ABCDEF").center();
LatexMathObject t2 = LatexMathObject.make("123456").center();
camera.zoomToObjects(t1, t2);
camera.scale(2);
TransformMathExpression tr = TransformMathExpression.make(10, t1, t2);
//If we don't map anything, all origin shapes are marked for removal and 
//all destiny shapes are marked for adding.

tr.setRemovingStyle(TransformMathExpression.RemoveType.FADE_OUT, 0);
tr.setRemovingStyle(TransformMathExpression.RemoveType.SHRINK_OUT, 1);
tr.setRemovingStyle(TransformMathExpression.RemoveType.MOVE_OUT_DOWN, 2);
tr.setRemovingStyle(TransformMathExpression.RemoveType.MOVE_OUT_LEFT, 3);
tr.setRemovingStyle(TransformMathExpression.RemoveType.MOVE_OUT_RIGHT, 4);
tr.setRemovingStyle(TransformMathExpression.RemoveType.MOVE_OUT_UP, 5);
        
tr.setAddingStyle(TransformMathExpression.AddType.FADE_IN, 0);
tr.setAddingStyle(TransformMathExpression.AddType.GROW_IN, 1);
tr.setAddingStyle(TransformMathExpression.AddType.MOVE_IN_DOWN, 2);
tr.setAddingStyle(TransformMathExpression.AddType.MOVE_IN_LEFT, 3);
tr.setAddingStyle(TransformMathExpression.AddType.MOVE_IN_RIGHT, 4);
tr.setAddingStyle(TransformMathExpression.AddType.MOVE_IN_UP, 5);
        
playAnimation(tr);
waitSeconds(3);

And finally, we show how the initial animation will look applying colors, mapping, and effects (again, this is not the optimal way from the didactic point of view):

LatexMathObject t1 = LatexMathObject.make("$x+2=0$");
LatexMathObject t2 = LatexMathObject.make("$x=-2$");
//Add some colors
t1.setColorsToIndices("darkolivegreen", 0);
t2.setColorsToIndices("darkolivegreen", 0);
t1.setColorsToIndices("maroon", 2);
t2.setColorsToIndices("maroon", 2, 3);

t2.alignCenter(1, t1, 3);//Align centers
camera.zoomToObjects(t1, t2);
TransformMathExpression tr = TransformMathExpression.make(5, t1, t2);
tr.map(0, 0);//Transforms orig-shape 0 to dst-shape 0
tr.map(1, 2)
    .addJumpEffect(t1.getHeight())
    .setTransformStyle(TransformMathExpression.TransformType.FLIP_VERTICALLY);//Transforms using a vertical flip orig-shape 1 to dst-shape 2 and adds a jump effect with the height of t1
tr.map(2, 3)
    .addJumpEffect(t1.getHeight());//Transforms orig-shape 2 to dst-shape 3 and adds a jump effect with the height of t1
tr.map(3, 1);//Transforms orig-shape 3 to dst-shape 1
tr.setRemovingStyle(TransformMathExpression.RemoveType.SHRINK_OUT, 4);
playAnimation(tr);
waitSeconds(3);

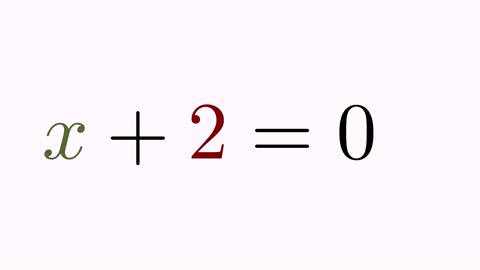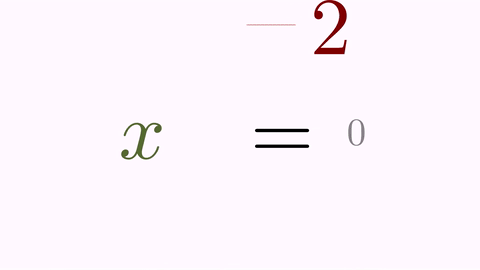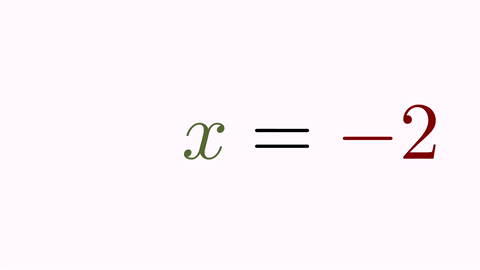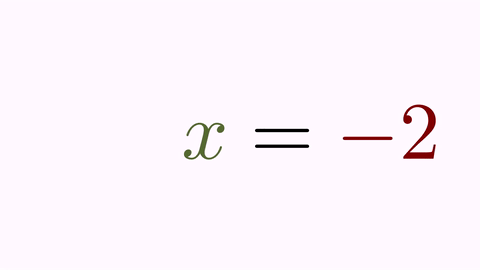
Cross out of parts of a formula

Since version 0.9.5, JMathAnim includes another animation that can be handy for manipulating equations called CrossOutMathElements. These animations, as their name suggests, cross out parts of a mathematical formula. Let’s see with a simple example:

LatexMathObject formula = LatexMathObject.make("$2\\over 2$");
add(formula);
camera.zoomToAllObjects();
CrossOutMathElements anim=CrossOutMathElements.make(1, formula, 0,2);//Cross out glyphs 0 and 2
playAnimation(anim);
waitSeconds(1);

Here is a GIF from the movie generated:

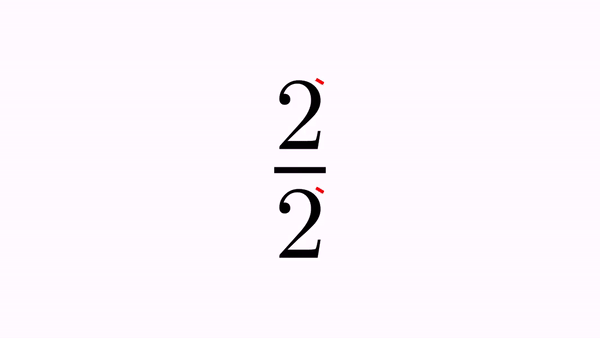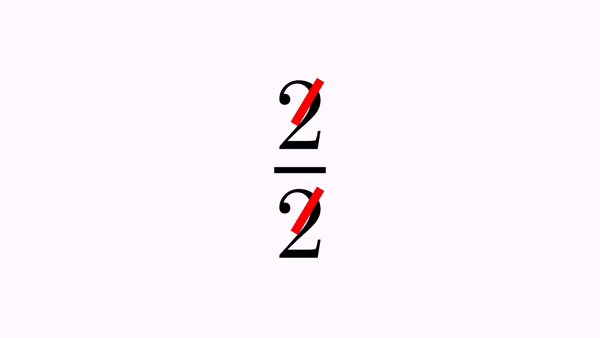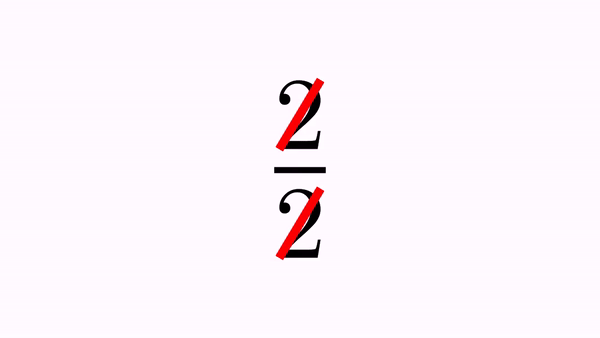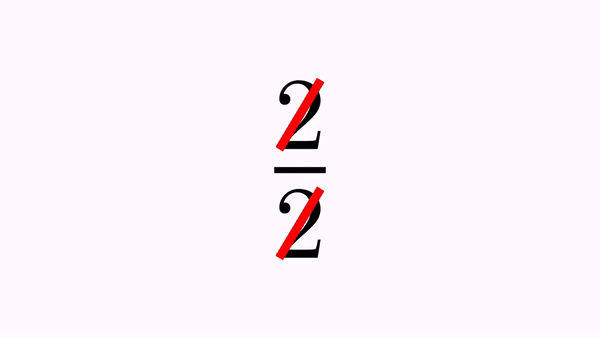
You can define which elements to cross out as usual, specifying the indices. There are 2 ways:

.addSmallCrosses(int...indices) generates one cross out for each individual glyph given by the index. This is the default behaviour for the static builder, so, another way to get the same result as before should be:

CrossOutMathElements anim=CrossOutMathElements.make(1, formula);
anim.addSmallCrosses(0,2);//Cross out glyphs 0 and 2

.addBigCross(int...indices) generates only one cross out that extends over all specified glyphs. For example:

LatexMathObject formula = LatexMathObject.make("$x-y+2y-y$");
add(formula);
camera.zoomToAllObjects();
CrossOutMathElements anim=CrossOutMathElements.make(1, formula);
anim.addBigCross(1,7);//A "big" cross out for -y+2y-y
playAnimation(anim);
waitSeconds(1);

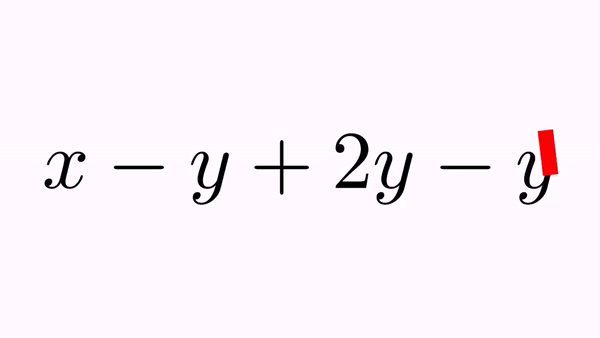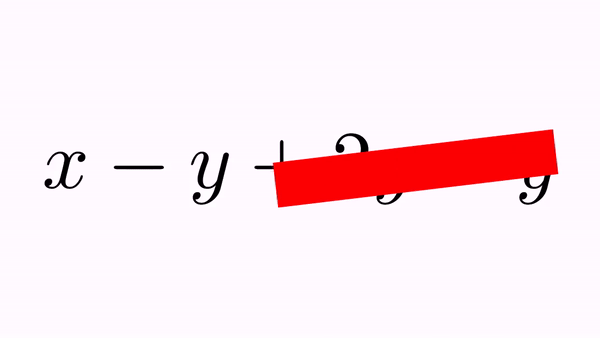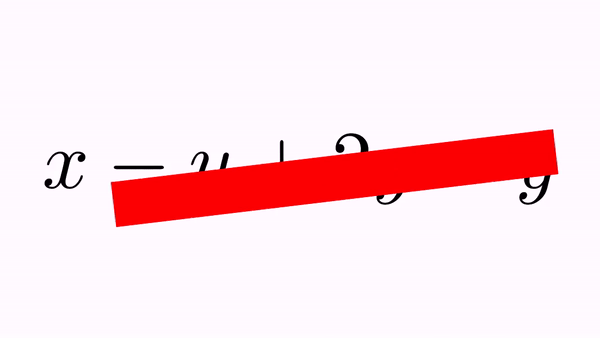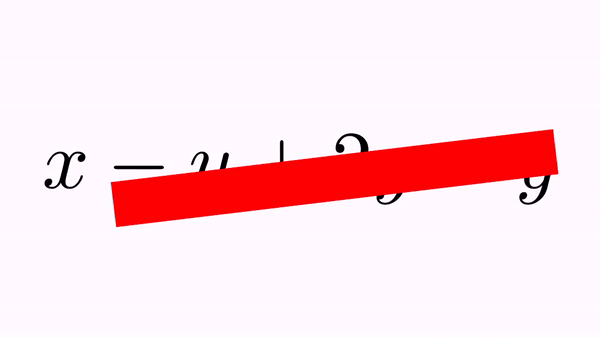
You can set appearance parameters for the drawn cross through the getMp() method defined in the animation. For example, if you want the cross out in the previous example to have 50% opacity and a black border, you can add the following lines to the previous code right before the playAnimation command:

anim.getMp().setFillColor(JMColor.parse("violet"))
			.setFillAlpha(.5)
			.setDrawColor(JMColor.parse("black"))
    		.setThickness(10d);
anim.crossRatioWidth(.1);//Width of cross out is 10% of length (default value is 5%)

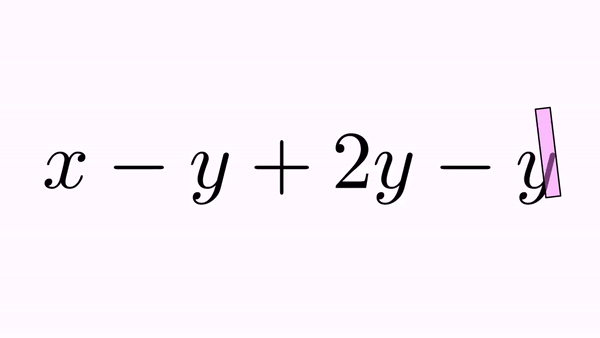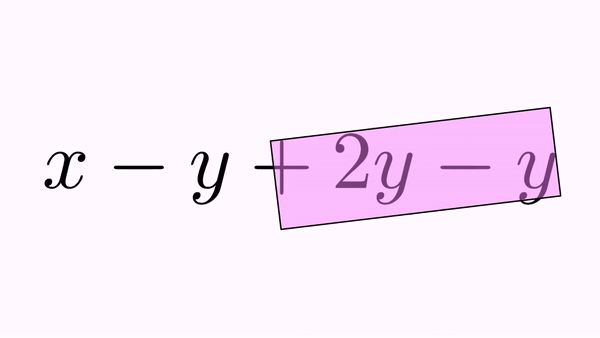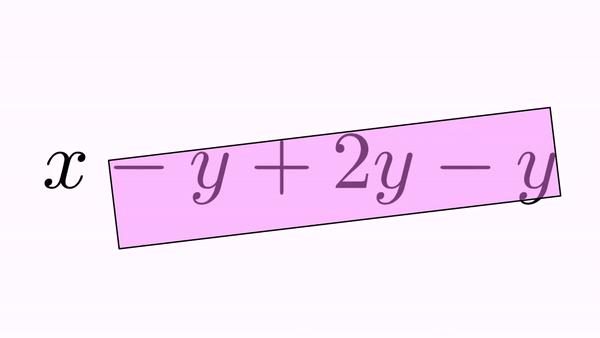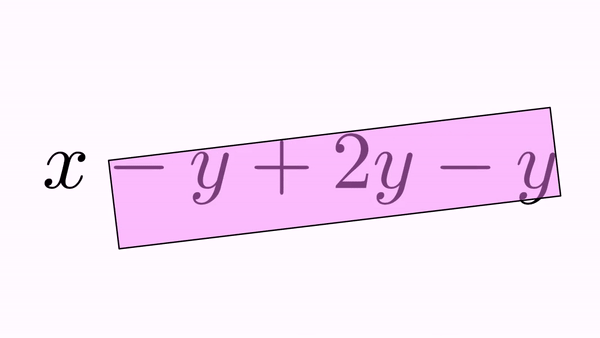
By default, all cross outs made to a formula become part of this formula. In the previous example, the big, violet cross out adds itself to the formula at the first free index, which is 8. This way, you can use them in further animations.

Another example, where we use 2 CrossOutMathElements animations, one with a different color. The first animation adds 2 crossouts at positions 13 and 14, and the second at positions 15 and 16. Remember that, although mapcommands may seem confusing, using the formulaHelper before makes things much clearer. We show here the indices of the formulas we are going to work with:

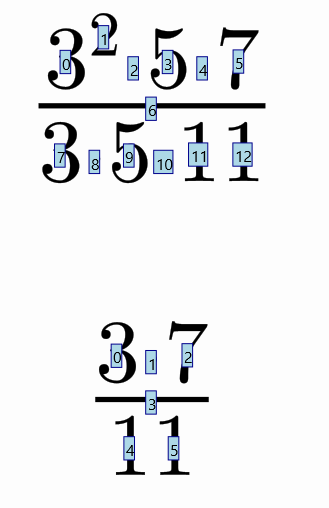
We want to perform a simplification, crossing out the exponent of the 3 in the numerator, with the 3 in the denominator, and later the 5 glyphs on both sides, and finally perform a transform to the simplified formula, removing all crossed out components. That’s what we do in the following code:

LatexMathObject eq1 = LatexMathObject.make("$3^2\\cdot 5\\cdot 7\\over 3\\cdot 5\\cdot 11$").center();
LatexMathObject eq2 = LatexMathObject.make("$3\\cdot 7\\over 11$").center();
eq1.scale(4);
eq2.scale(4);
add(eq1);
waitSeconds(1);

//Cross out the exponent of numerator and the 3 of denominator
CrossOutMathElements cross1 = CrossOutMathElements.make(1, eq1, 1, 7);
cross1.getMp().loadFromStyle("solidred");
playAnimation(cross1);
waitSeconds(.5);

//Cross out the 5 of numerator and denominator
CrossOutMathElements cross2 = CrossOutMathElements.make(1, eq1, 3, 9);
cross2.getMp().loadFromStyle("solidgreen");
cross2.addDelayEffect(.2);
playAnimation(cross2);

waitSeconds(1);
TransformMathExpression anim = TransformMathExpression.make(2, eq1, eq2);
anim.map(0, 0);
anim.map(4, 1);
anim.map(5, 2);
anim.map(6, 3);
anim.map(11, 4);
anim.map(12, 5);
anim.setDefaultRemovingStyle(TransformMathExpression.RemoveType.FADE_OUT);

//The crossed out parts (and the crosses themselves) are removed moving themselves up (numerator) or down (denominator)
anim.setRemovingStyle(TransformMathExpression.RemoveType.MOVE_OUT_UP, 1, 3, 13, 15);
anim.setRemovingStyle(TransformMathExpression.RemoveType.MOVE_OUT_DOWN, 7, 9, 14, 16);

playAnimation(anim);
waitSeconds(1);